Problemet e ndryshme implikojnë përdorimin e teknikave dhe algoritmeve të ndryshme për zgjidhjen e tyre. Parakusht i domosdoshëm për dizajnimin e një zgjidhjeje është njohja e detajuar e natyrës dhe e problemit përkatës. Nën supozimin e plotësimit të këtij kushti, pikënisja për zgjidhjen e një problemi përmes një algoritmi të caktuar është modelimi i atij problemi. Me modelim ose paraqitje të problemit i referohemi paraqitjes së problemit përmes strukturave të caktuara të të dhënave. Të rrallë janë rastet e përdorimit të algoritmeve për gjetje të zgjidhjeve të cilat nuk janë të destinuara të implementohen në ndonjë program kompjuterik, gjegjësisht gjuhë programuese. Kjo është edhe arsyeja pse direkt u kalua në paraqitjen si strukturë e të dhënave, gjegjësisht paraqitjen si e dhënë digjitale e njëherit edhe qëllimi i këtij artikulli të shkurtë është që në këtë aspekt ta trajtojë teknikën “Përçaj dhe sundo”.

Një modelim i mirë i problemit jep përparësinë e idejimit më të shpejtë të zgjidhjes dhe shpeshherë e orienton drejt saj. Zgjidhja e problemit paraqet gjendjen e dëshiruar (nga anglishtja target state) të problemit. Kjo zakonisht përcaktohet përmes ndonjë modeli ose rregullave të caktuara. Rruga deri në zgjidhje i ka hapat e vet të definuar saktë dhe teknikën përkatëse poashtu të definuar saktë. Një prej teknikave më të shpeshta të përdorura nga algoritmet e ndryshme është edhe teknika “Përçaj dhe sundo”. E bazuar në parimin socio-politik të përcarjes ose ndarjes dhe sundimit, teknika ka për qëllim që një problem ta ndajë në pjesëza të natyrës së njëjtë, të ofrohet zgjidhja për këto dhe në fund bashkimin e këtyre të fundit në zgjidhjen totale. Për të ilustruar këtë teknikë do të trajtohet problemi i njohur si “Tromino Puzzle” dhe algoritmi “Merge sort”.

Tromino Puzzle paraqet një matricë të rendit 2n ku n>0 e cila duhet të mbushet me “tromino” përveç një fushe e cila duhet të lihet e lirë. Fushën e lirë mund ta përcaktojmë në formë të rastësishme ose qëllimtazi. Në figurën në vijim është dhënë një shembull se çka paraqet “tromino” dhe si duket një matricë e plotësuar.

Figura 1: Shembull i matricës së plotësuar dhe i një trominoje

Gjendja e dëshiruar për këtë problem është e një matricë e cila ka të pa plotësuar vetëm një qeli, pozita e së cilës siç u tha mund të zgjidhet ose gjenerohet në formë të rastësishme. Modelimi i këtij problemi është deri diku intuitiv. Vetë paraqitja grafike na asocon në paraqitjen përmes vargjeve dydimensionale ose matricave. Për të aplikuar teknikën “Përçaj dhe sundo”, na duhet të analizojmë se cili është rasti bazik për të cilin kemi njohuri ose mund ta zgjidhim përmes krahasimeve bazike. Rasti më i thjeshtë është rasti kur matrica është e madhësisë 2x2. Në atë rast kontrollojmë përmes dy unazave se në cilën pozitë gjendet hapësira e lirë dhe në të tjerat e vendosim “trominon”.

Për të ardhur në këtë rast bazik na duhet që në formë rekursive të bëjmë ndarjen e matricës në 4 nën matrica (secili kuadrant një matricë në vete) derisa rangu i matricës të jetë 2x2 që paraqet rastin bazë (edhe për algoritëm edhe për rekursivitet). Gjatë ndarjes së matricës, kontrollojmë se në cilën prej 4 nën matricave gjendet hapësira e lirë. Nën matrica e cila e përmbanë hapësirën e lirë mbetet siç është ndërkaq të tjerat lidhen përmes një “trominoje”. Kjo ndodhë derisa të vijmë tek rasti bazik që u përmend. Nga aty në formë rekursive (tash mbrapsht) bëhet plotësimi i matricës. Në vijim është paraqitur me shembull të ilustruar.

Hapi i parë – ndarja në nën matrica dhe lidhja përmes “trominos” e nën matricave ku nuk ndodhet hapësira e lirë

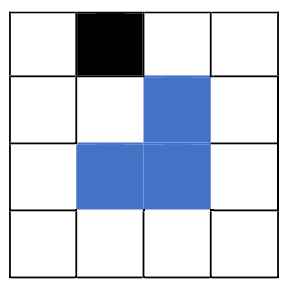
Hapi i dytë – plotësimi i rasteve bazike

Hapi i tretë – bashkimi në një zgjidhje të vetme

Pseudokodi për realizimin e këtij algoritmi duket si në vijim.

Funksioni Tromino(matrica, dimensioni)

-  Nëse dimensioni është baraz me 2

o  Plotëso rastin bazik

-  Përndryshe

o  Ndaj matricën në 4 nën matrica

o  Kontrollo në cilën nën matricë gjendet hapësira e lirë

o  Ndërlidh nën matricat tjera përmes një “trominoje”

o  Për secilën nën matricë thirr funksionin rekursiv Tromino(nën matrica, dimensioni i ri)

-  Bashko nën matricat

-  Ktheje rezultatin e bashkimit të nënmatricave

Ndjekja e këtyre hapave, gjegjësisht kësaj strategjie na garanton plotësimin e secilës matricë valide të çfarëdo rangu për problemin në fjalë.

Mbi teknikën e njëjtë është i ndërtuar edhe një prej algoritmeve më të përdorura për sortim, algoritmi “Merge sort”. Ky algoritëm përdoret për renditjen ose sortimin e vargjeve të ndryshme. Pseudokodi i këtij algoritmi mund të tingëllojë pak i komplikuar andaj qëllimisht është shmangur në këtë artikull. Sidoqoftë i njëjti mund të gjendet në thuajse çdo libër (përfshirë atë të vendosur si bibliografi) që trajton kompleksitetin dhe dizajnin e algoritmeve. Algoritmi në fjalë punon në atë formë që e ndanë vargun përgjysmë në formë rekursive derisa të arrin në dy vargje me nga një anëtar. Nga ai hap bëhet renditja e tyre përmes krahasimit të elementeve të anës së majtë dhe të djathtë e më pastaj edhe bashkimi i tyre poashtu në formë rekursive, deri në plotësimin e gjatësisë së vargut fillestar. Grafikisht është ilustruar në vijim.

Figura 2: Ilustrimi i parimit të punës së algoritmit Merge Sort

Si konkluzion mund të thuhet se teknika “Përçaj dhe sundo” përbën një teknikë të thjeshtë në implementim por shumë efikase dhe që gjen zbatim në një gamë të gjerë problemesh. Shumë algoritme të njohura (sidomos për renditje ose sortim) përdorin këtë teknikë në variante të ndryshme me qëllim zvogëlimin e kompleksitetit kohor të ekzekutimit të algoritmeve përkatëse. Definitivisht teknikë e rekomanduar në problemet tek natyra e të cilëve mund të gjejë zbatim.

Bibliografia

Levitin A, Introduction to the design and analysis of algorithms – 3rd Edition, 2012, Pearson Education