Detyra “Friends fruit cocktail” statistikisht ka dalur të jetë detyra më e vështirë e garës Gjirafa#. Kjo sepse është provuar nga shumë pjesëmarrës, por nuk është zgjidhur nga asnjëri. Poashtu, pas garës kemi marrë edhe shumë kërkesa për t’i parë të gjithë test-cases së detyrës, sepse për shumë persona zgjidhja e tyre dështonte në disa test-case të caktuar. Kjo ka qenë edhe një prej arsyeve kryesore pse kemi vendosur t’i publikojmë zgjidhjet për të gjitha detyrat. 

Për ata që nuk e kanë parë, përshkrimin e plotë të detyrës mund ta lexoni në HackerRank përmes këtij linku: https://www.hackerrank.com/contests/gjirafa/challenges/friends-fruit-cocktail (ju rekomandojmë ta lexoni detyrën origjinale para se të vazhdoni me pjesën tjetër të këtij artikulli).

Siq mund ta shihni nga teksti, në këtë detyrë kemi një sfidë që ka të bëjë me optimizime në kohë të ekzekutimit. Arsyeja pse kjo detyrë nuk është arritur të zgjidhet nga asnjë prej garuesve është për shkak se disa nga test-cases përmbajnë një numër të lartë të opsioneve që rezultojnë në një numër shumë të madh të kombinimeve ndërmjet tyre. Kjo ka shkaktuar që shumë prej zgjidhjeve të postuara të dështojnë për shkak të limitit kohor të ekzekutimit.

Ju keni një numër të caktuar të frutave që duhet t’i kombinoni për të bërë një koktell frutash. Por, disa nga shokët/shoqet tuaj nuk e pëlqejnë ndonjë frut dhe nuk e konsumojnë asnjë koktell që përmban atë frut të caktuar. Detyra e juaj është që të gjeni kombinimin më të mirë të frutave duke u munduar të përdorni në minimum një numër të caktuar të tyre dhe të plotësoni dëshirat e sa më shumë personave. Kjo do të thotë se ka raste ku ju duhet të sakrifikoni dëshirat e një personi të caktuar për të përmbushur numrin minimal të frutave. 

Duke u bazuar në këto kërkesa, zgjidhja më e drejtëpërdrejtë është që të krijoni të gjitha kombinimet e mundshme të frutave dhe më pas të iteroni nëpër të gjithë këto kombinime dhe të zgjedhni se cili prej tyre i plotëson dëshirat e sa më shumë personave duke e arritur apo kaluar edhe numrin minimal të frutave të përdorur. Por, problemi me këtë zgjidhje qëndron në faktin se disa nga test-cases kanë një numër të madh të frutave, që mund të krijojnë një numër shumë të madh të iterimeve, e cila ndikon edhe në kalimin e limitit kohor të ekzekutimit të kodit.

Për të zgjidhur në kohë detyrën edhe për keto raste, duhet të përdorim një qasje më të optimizuar. Disa nga teknikat e përdorura për zgjidhjen e detyrës bazohen në “Bitmasking and Dynamic Programming”, ku një shpegim rreth kësaj mund të gjeni në këtë link: 

https://www.geeksforgeeks.org/bitmasking-and-dynamic-programming-set-1-count-ways-to-assign-unique-cap-to-every-person/

Që të shpjegojmë më lehtë zgjidhjen e detyrë, po e marrim si shembull të zgjidhjes test-case-in e parë të detyrës. Ky test-case ka si input:

apple orange strawberry cherry
2
5
apple orange
apple cherry
strawberry orange
cherry
apple

Në këtë test-case kemi të bëjmë më 4 fruta të ndryshme dhe 5 persona me preferenca të caktuara. Fillojmë duke e krijuar një matricë me vlera boolean ku çdo rresht i detyrës reprezenton një frut dhe secila kolone reprezenton se a pëlqehet ai frut nga ai person, me vlerat 1 (true) dhe 0 (false). Nga test case kemi matricën:

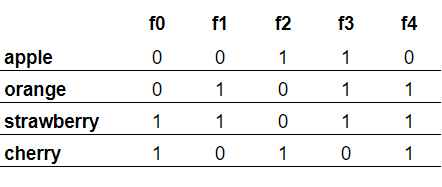
Poashtu, e dijm se një set me N elemente ka në total 2^N subseta të ndryshme. Kjo do të thotë se për rastin tonë me 5 persona, kemi 32 kombinime të ndryshme të tyre. Këto  kombinime mund t’i paraqesim përmes një vargu të numrave, ku reprezentimi i tyre binar tregon edhe kombinimin e personave:

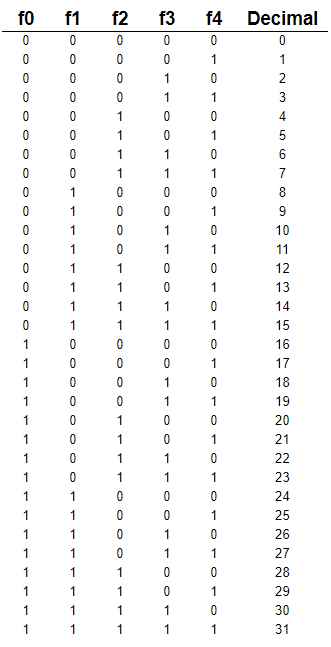
Tani mund të bëjmë një iterim mbi të gjitha subsets dhe të bëjmë krahasimet me preferencat e secilit person për secilin frut. Nga ky iterim mund ta vërejmë për secilin subset sa fruta mund të përdoren dhe rrjedhimisht edhe sa persona bëjnë pjesë në atë subset. Nëse e marrim si shembull subset-in me vlerë decimale 10, atëherë kemi:

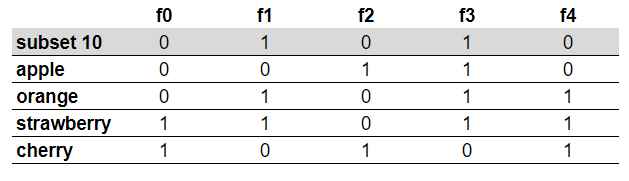
Nga fotoja e vërejmë se frutat që mund të përdoren në këtë subset janë: “orange” dhe “strawberry”. Poashtu nga subset e vërejmë se ky subset përmban 2 persona, personin “f1” dhe personin “f3”. Kjo do të thotë se ky subset e arrin limitin prej minimum 2 frutave, por përfshin vetëm 2 persona, që nuk është zgjidhja më e mirë për këtë detyrë. Për të gjetur zgjidhjen më të mirë, duhet të bëjmë iteriminim mbi të gjithë subset-a dhe të gjejmë subset-in që arrin një minimum prej 2 frutave dhe ka numrin më të madh të personave. 

Siç e kemi cekur më lartë, kjo detyrë përmban disa test-case që kanë numër të madh të frutave dhe personave. Kjo ndikon në krijimin e një matrice të madhe, prandaj duhet ta optimizojmë këtë pjesën e validimit të secilit subset. Për të bërë këtë mund të përdorim operacionin logjik XOR si dhe mbledhjen. Mënyra më e shpejtë për të validuar se një subset mund të përdorë një frut apo jo, është duke ndjekur hapat:

1. Përmbysim vlerat e preferencave të frutave në raport me personat (nga 1 në 0 dhe anasjelltas)
2. Kthejmë në anën e kundërt renditjen e vlerave (p.sh nga 1, 0, 0 në 0, 0, 1)
3. Përformojmë operacionin XOR ndërmjet vlerave të subsetit dhe vlerave nga pika 2
4. Përformojmë mbledhjen në mes të vlerave të subsetit dhe vlerave nga pika 2
5. Nëse rezultati nga pika 3 është i barabartë me rezultatin nga pika 4 atëherë ai frut mund të përdoret në subsetin e caktuar
6. Performojmë të njejtën edhe për frutat tjera dhe mbledhim sa fruta janë valide për subsetin e caktuar

Nëse provojme të vizualizojmë këtë proces, atëhere kemi:

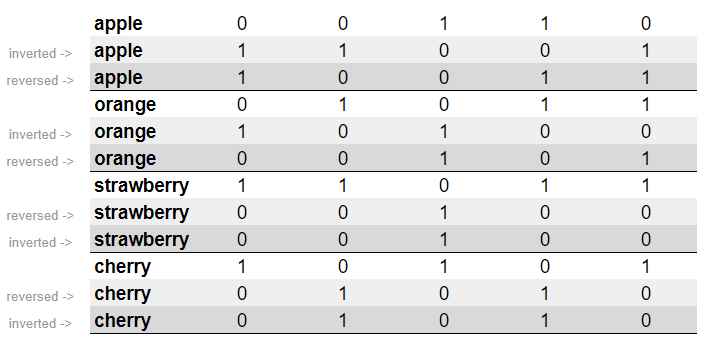
Dhe nga operacionet e performuara për frutin “apple” kemi:

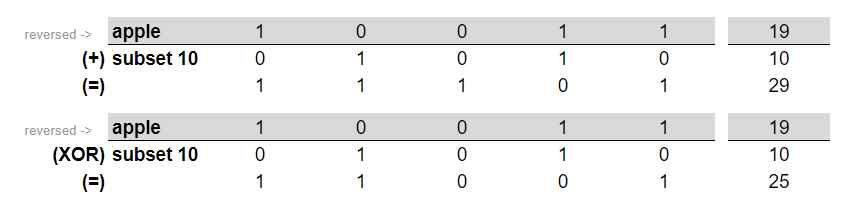
E vërejme se rezultati i mbledhjes dhe XOR-it nuk janë të barabartë, rrjedhimisht ky frut nuk mund të përdoret në këtë subset. Vazhdojme procesimin për frutin “orange”:

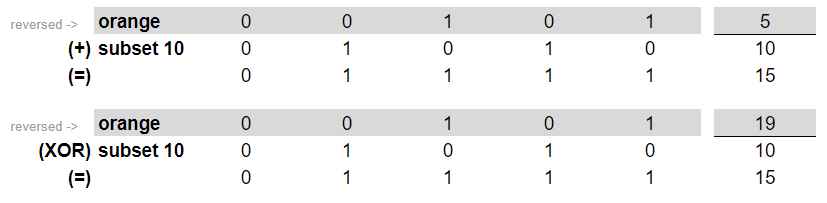
E vërejme se rezultati i mbledhjes dhe XOR-it është i barabartë, rrjedhimisht ky frut mund të përdoret në këtë subset. Vazhdojmë procesimin edhe për frutat e mbetur.

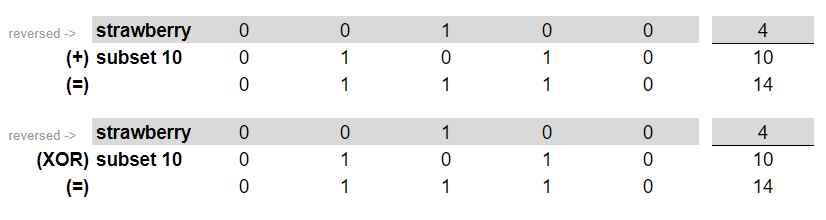
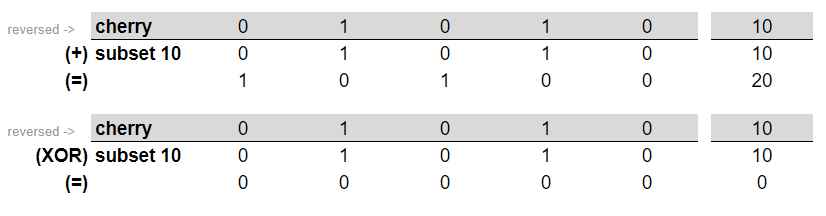
Kjo e vërteton se duke përdorur këto dy operacione mund të gjëjmë se cilat fruta mund të përdoren për subseta të caktuar. Arsyeja pse i kemi vendosur edhe vlerat decimale në seciën foto të operacionit është për shkak se ne mund të performojmë këtë operacion edhe pa përdorur varg të bitave, por duke përdorur direkt në numra decimal (integer). Mbledhja e numrave është veçse triviale, por operacioni XOR në numra mund të bëhet duke përdorur nr1 ^ nr2. Këtu qëndron edhe sekreti i kësaj qasje, për shkak se na lejon të përformojmë të gjitha këto operacione në një kohë shumë të shkurtër. Për çdo subset i numërojmë të gjitha frutat që mund të përdoren. Për të numëruar numrin e personave, përformojmë operacionin BitCount në atë numër. 

Pasi që e shpjeguam algoritmin e zgjidhjes, tani po e paraqesim edhe zgjidhjen në kod, në gjuhën C#:

using System;

public class Solution 
{
    public static void Main(String[] args) 
    {
        var availableFruits = Console.ReadLine().Split(' ');
        int f = Convert.ToInt32(Console.ReadLine());
        int n = Convert.ToInt32(Console.ReadLine());

        var friendsDislikings = new string[n];
        for (int i = 0; i < n; i++)
            friendsDislikings[i] = Console.ReadLine();

        int nrOfFruits = availableFruits.Length;
        var maxSubsets = (int)Math.Pow(2, n);
        var subsetResults = new int[maxSubsets];

        var matrix = new bool[nrOfFruits, n];
        for (int i = 0; i < nrOfFruits; i++)
        {
            for (int j = 0; j < n; j++)
            {
                matrix[i, j] = true;
            }
        }

        for (int i = 0; i < n; i++)
        {
            var dislikings = friendsDislikings[i].Split(' ');
            for (int j = 0; j < dislikings.Length; j++)
            {
                for (int l = 0; l < nrOfFruits; l++)
                {
                    if (dislikings[j] == availableFruits[l])
                    {
                        matrix[l, i] = false;
                    }
                }
            }
        }

        for (int i = 0; i < nrOfFruits; i++)
        {
            var incrementValue = 1;
            var bitSet = 0;
            for (int j = 0; j < n; j++)
            {
                if (!matrix[i, j])
                {
                    bitSet += incrementValue;
                }
                incrementValue *= 2;
            }

            for (int j = 0; j < maxSubsets; j++)
            {
                if ((j ^ bitSet) == (j + bitSet))
                {
                    subsetResults[j]++;
                }
            }
        }

        var finalAnswer = 0;
        for (int j = 0; j < maxSubsets; j++)
        {
            if ((subsetResults[j] >= f) && (BitCount(j) > finalAnswer))
            {
                finalAnswer = BitCount(j);
            }
        }
        Console.WriteLine(finalAnswer);
    }
        
    public static int BitCount(int n)
    {
        var count = 0;
        while (n != 0)
        {
            count++;
            n &= (n - 1);
        }
        return count;
    }
}

p.s kjo zgjidhje bazohet në një zgjidhje të bërë në një nga platformat e famshme të garave të programimit: Topcoder